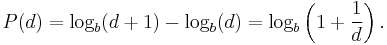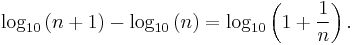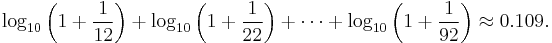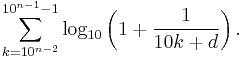Benford's law

For the tongue-in-cheek "law" about controversy, see Benford's law of controversy.
Rectangle with offset bolded axis in lower left, and light gray lines representing logarithms
A logarithmic scale bar. Picking a random x position on this number line, roughly 30% of the time the first digit of the number will be 1 (the widest band of each power of ten).

Benford's law, also called the first-digit law, states that in lists of numbers from many (but not all) real-life sources of data, the leading digit is distributed in a specific, non-uniform way. According to this law, the first digit is 1 almost one third of the time, and larger digits occur as the leading digit with lower and lower frequency, to the point where 9 as a first digit occurs less than one time in twenty. This distribution of first digits arises whenever a set of values has logarithms that are distributed uniformly, as is approximately the case with many measurements of real-world values.

This counter-intuitive result has been found to apply to a wide variety of data sets, including electricity bills, street addresses, stock prices, population numbers, death rates, lengths of rivers, physical and mathematical constants, and processes described by power laws (which are very common in nature). The result holds regardless of the base in which the numbers are expressed (except for trivial bases), although the exact proportions change.

It is named after physicist Frank Benford, who stated it in 1938,[1] although it had been previously stated by Simon Newcomb in 1881.[2]

Contents

Mathematical statement

A sequence of decreasing blue bars against a light gray grid background.
Benford's distribution

More precisely, Benford's law states that the leading digit d (d ∈ {1, …, b − 1} ) in base b (b > 2) occurs with probability

P(d)=\log_b(d+1)-\log_b(d)=\log_b \left(1+\frac{1}{d}\right).

This quantity is exactly the space between d and d + 1 in a logarithmic scale. (Note that the limitation b>2 excludes the trivial cases of binary (b=2), in which all numbers begin with 1, and unary systems (b=1) in which the number d is represented by d tally marks.)

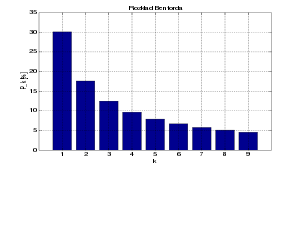
In base 10, the leading digits have the following distribution by Benford's law, where d is the leading digit and p the probability:

d p
1 30.1%
2 17.6%
3 12.5%
4 9.7%
5 7.9%
6 6.7%
7 5.8%
8 5.1%
9 4.6%

Example

Distribution of first digits (in %, red bars) in the population of the 237 countries of the world. Black dots indicate the distribution predicted by Benford's law.

Examining a list of the heights of the 60 tallest structures in the world by category shows that 1 is by far the most common leading digit, irrespective of the unit of measurement:

Leading digit meters feet
Count % Count %
1 26 43.3% 18 30.0%
2 7 11.7% 8 13.3%
3 9 15.0% 8 13.3%
4 6 10.0% 6 10.0%
5 4 6.7% 10 16.7%
6 1 1.7% 5 8.3%
7 2 3.3% 2 3.3%
8 5 8.3% 1 1.7%
9 0 0.0% 2 3.3%

Explanations

Benford's law has been explained in various ways.

Outcomes of exponential growth processes

The precise form of Benford's law can be explained if one assumes that the logarithms of the numbers are uniformly distributed; for instance that a number is just as likely to be between 100 and 1000 (logarithm between 2 and 3) as it is between 10,000 and 100,000 (logarithm between 4 and 5). For many sets of numbers, especially ones that grow exponentially such as incomes and stock prices, this is a reasonable assumption.

For example, if a quantity increases continuously and doubles every year, then it will be twice its original value after one year, four times its original value after two years, eight times its original value after three years, and so on. When this quantity reaches a value of 100, the value will have a leading digit of 1 for a year, reaching 200 at the end of the year. Over the course of the next year, the value increases from 200 to 400; it will have a leading digit of 2 for a little over seven months, and 3 for the remaining five months. In the third year, the leading digit will pass through 4, 5, 6, and 7, spending less and less time with each succeeding digit, reaching 800 at the end of the year. Early in the fourth year, the leading digit will pass through 8 and 9. The leading digit returns to 1 when the value reaches 1000, and the process starts again, taking a year to double from 1000 to 2000. From this example, it can be seen that if the value is sampled at uniformly distributed random times throughout those years, it is more likely to be measured when the leading digit is 1, and successively less likely to be measured with higher leading digits.

This example makes it plausible that data tables that involve measurements of exponentially growing quantities will agree with Benford's Law. But the law also appears to hold for many cases where an exponential growth pattern is not obvious.

Frequency of first significant digit of physical constants plotted against Benford's Law.

Scale invariance

The law can alternatively be explained by the fact that, if it is indeed true that the first digits have a particular distribution, it must be independent of the measuring units used. This means that if one converts from e.g. feet to yards (multiplication by a constant), the distribution must be unchanged — it is scale invariant, and the only distribution that fits this is one whose logarithm is uniformly distributed.

For each positive integer n, this graph shows the probability that a random integer between 1 and n starts with each of the nine possible digits. For any particular value of n, the probabilities do not precisely satisfy Benford's law; however, looking at a variety of different values of n and averaging the probabilities for each, the resulting probabilities do exactly satisfy Benford's law.


For example, the first (non-zero) digit of the lengths or distances of objects should have the same distribution whether the unit of measurement is feet, yards, or anything else. But there are three feet in a yard, so the probability that the first digit of a length in yards is 1 must be the same as the probability that the first digit of a length in feet is 3, 4, or 5. Applying this to all possible measurement scales gives a logarithmic distribution, and combined with the fact that log10(1) = 0 and log10(10) = 1 gives Benford's law. That is, if there is a distribution of first digits, it must apply to a set of data regardless of what measuring units are used, and the only distribution of first digits that fits that is the Benford Law.

Multiple probability distributions

Note that for numbers drawn from certain distributions, for example IQ scores, human heights or other variables following normal distributions, the law is not valid. However, if one "mixes" numbers from those distributions, for example by taking numbers from newspaper articles, Benford's law reappears. This can also be proven mathematically: if one repeatedly "randomly" chooses a probability distribution and then randomly chooses a number according to that distribution, the resulting list of numbers will obey Benford's law.[3][4]

Applications

In 1972, Hal Varian suggested that the law could be used to detect possible fraud in lists of socio-economic data submitted in support of public planning decisions. Based on the plausible assumption that people who make up figures tend to distribute their digits fairly uniformly, a simple comparison of first-digit frequency distribution from the data with the expected distribution according to Benford's law ought to show up any anomalous results.[5] Following this idea, Mark Nigrini showed that Benford's law could be used as an indicator of accounting and expenses fraud.[6] In the United States, evidence based on Benford's law is legally admissible in criminal cases at the federal, state, and local levels.[7]

Benford's law has been invoked as evidence of fraud in the 2009 Iranian elections.[8]

In June 2010, consultants working for political website Daily Kos used Benford's law, among other tools, to find serious flaws in the data collected by polling company Research 2000 (R2K). This led to the termination of R2K's contract with Daily Kos, and possible litigation.[9]

Limitations

Benford's law can only be applied to data which is distributed across multiple orders of magnitude. For instance, one might expect that Benford's law would apply to a list of numbers representing the populations of UK villages beginning with 'A', or representing the values of small insurance claims. But if a "village" is a settlement with population between 300 and 999, or a "small insurance claim" is a claim between $50 and $100, then Benford's law will not apply.[10][11]

Consider the probability distributions shown below, plotted on a log scale.[12] In each case, the total area in red is the relative probability that the first digit is 1, and the total area in blue is the relative probability that the first digit is 8.

A broad probability distribution on a log scale
A narrow probability distribution on a log scale

For the left distribution, the size of the areas of red and blue are approximately proportional to the widths of each red and blue bar. Therefore the numbers drawn from this distribution will approximately follow Benford's law. On the other hand, for the right distribution, the ratio of the areas of red and blue is very different from the ratio of the widths of each red and blue bar. Rather, the relative areas of red and blue are determined more by the height of the bars than the widths. The heights, unlike the widths, do not satisfy the universal relationship of Benford's law; instead, they are determined entirely by the shape of the distribution in question. Accordingly, the first digits in this distribution do not satisfy Benford's law at all.[11]

Thus, real-world distributions that span several orders of magnitude rather smoothly like the left distribution (e.g. income distributions, or populations of towns and cities) are likely to satisfy Benford's law to a very good approximation. On the other hand, a distribution that covers only one or two orders of magnitude, like the right distribution (e.g. heights of human adults, or IQ scores) is unlikely to satisfy Benford's law well.[10][11]

History

The discovery of this fact goes back to 1881, when the American astronomer Simon Newcomb noticed that in logarithm books (used at that time to perform calculations), the earlier pages (which contained numbers that started with 1) were much more worn than the other pages.[2] Newcomb's published result is the first known instance of this observation and includes a distribution on the second digit, as well. Newcomb proposed a law that the probability of a single number being the first digit of a number (let such a first digit be N) was equal to log(N + 1) − log(N).

The phenomenon was rediscovered in 1938 by the physicist Frank Benford,[1] who checked it on a wide variety of data sets and was credited for it. In 1995, Ted Hill proved the result about mixed distributions mentioned above.[4] The discovery was named after Benford making it an example of Stigler's law.

Generalization to digits beyond the first

It is possible to extend the law to digits beyond the first.[13] In particular, the probability of encountering a number starting with the string of digits n is given by:

\log_{10}\left(n+1\right)-\log_{10}\left(n\right)=\log_{10}\left(1 +\frac{1}{n}\right).

(For example, the probability that a number starts with the digits 3,1,4 is log10(1 + 1/314) ≈ 0.0014.) This result can be used to find the probability that a particular digit occurs at a given position within a number. For instance, the probability that a "2" is encountered as the second digit is[13]

\log_{10}\left(1 +\frac{1}{12}\right)+\log_{10}\left(1 +\frac{1}{22}\right)+\cdots+\log_{10}\left(1 +\frac{1}{92}\right) \approx 0.109.

And the probability that d (d = 0, 1, ..., 9) is encountered as the n-th (n > 1) digit is

\sum_{k=10^{n-2}}^{10^{n-1}-1} \log_{10}\left(1 + \frac{1}{10k+d}\right).

The distribution of the n-th digit, as n increases, rapidly approaches a uniform distribution with 10% for each of the ten digits.[13]

In practice, applications of Benford's law for fraud detection routinely use more than the first digit.[6]

See also

Notes

  1. ↑ 1.0 1.1 Frank Benford (March 1938). "The law of anomalous numbers". Proceedings of the American Philosophical Society 78 (4): 551–572. http://links.jstor.org/sici?sici=0003-049X(19380331)78%3A4%3C551%3ATLOAN%3E2.0.CO%3B2-G.  (subscription required)
  2. ↑ 2.0 2.1 Simon Newcomb (1881). "Note on the frequency of use of the different digits in natural numbers". American Journal of Mathematics (American Journal of Mathematics, Vol. 4, No. 1) 4 (1/4): 39–40. doi:10.2307/2369148. http://jstor.org/stable/2369148.  (subscription required)
  3. ↑ Theodore P. Hill (July–August 1998). "The first digit phenomenon" (PDF). American Scientist 86: 358. http://www.tphill.net/publications/BENFORD%20PAPERS/TheFirstDigitPhenomenonAmericanScientist1996.pdf. 
  4. ↑ 4.0 4.1 Theodore P. Hill (1995). "A Statistical Derivation of the Significant-Digit Law" (PDF). Statistical Science 10: 354–363. http://www.tphill.net/publications/BENFORD%20PAPERS/statisticalDerivationSigDigitLaw1995.pdf. 
  5. ↑ Varian, Hal. "Benford's law". The American Statistician 26: 65. 
  6. ↑ 6.0 6.1 Mark J. Nigrini (May 1999). "I've Got Your Number". Journal of Accountancy. http://www.journalofaccountancy.com/Issues/1999/May/nigrini. 
  7. ↑ "From Benford to Erdös". Radio Lab. 2009-09-30. No. 2009-10-09.
  8. ↑ Stephen Battersby Statistics hint at fraud in Iranian election New Scientist 24 June 2009
  9. ↑ Moulitsas, Markos (6/29/2010). "Research 2000: Problems in plain sight" (HTML). DailyKos. http://www.dailykos.com/story/2010/6/29/880179/-Research-2000:-Problems-in-plain-sight. 
  10. ↑ 10.0 10.1 See [1], in particular [2].
  11. ↑ 11.0 11.1 11.2 Fewster, R. M. (2009). "A simple explanation of Benford's Law". The American Statistician 63 (1): 26–32. doi:10.1198/tast.2009.0005 
  12. ↑ Note that if you have a regular probability distribution (on a linear scale), you have to multiply it by a certain function to get a proper probability distribution on a log scale: The log scale distorts the horizontal distances, so the height has to be changed also, in order for the area under each section of the curve to remain true to the original distribution. See, for example, [3]
  13. ↑ 13.0 13.1 13.2 Theodore P. Hill, "The Significant-Digit Phenomenon", The American Mathematical Monthly, Vol. 102, No. 4, (Apr., 1995), pp. 322–327. Official web link (subscription required). Alternate, free web link.

References

External links

General audience

More mathematical

Probability distributions
 
Discrete univariate with finite support
Benford · Bernoulli · Beta-binomial  · binomial · categorical · hypergeometric · Poisson binomial · Rademacher · discrete uniform · Zipf · Zipf-Mandelbrot